幾何ベクトルの一次結合と基底

2022-05-04

幾何ベクトルの一次結合

幾何ベクトルの空間には「加法」と「スカラー倍」が定義されています。 ですから、例えば、2つのベクトル \(\boldsymbol{a},\boldsymbol{b}\) と2つの数 \(x,y\) から
\[ x\,\boldsymbol{a} + y\,\boldsymbol{b} \] というベクトルを作ることができます。

もっと一般に、\(n\) 個の幾何ベクトル \(\boldsymbol{a}_1, \boldsymbol{a}_2,\ldots, \boldsymbol{a}_n\) と \(n\) 個の数 \(x_1, x_2, \ldots, x_n\) から \[ x_1\boldsymbol{a}_1 + x_2\boldsymbol{a}_2 + \ldots + x_n\boldsymbol{a}_n \] という幾何ベクトルを作ることができます。 このようにして作られるベクトルを \(\boldsymbol{a}_1, \boldsymbol{a}_2,\ldots, \boldsymbol{a}_n\) の一次結合といいます。

補足：一次結合は線型結合とも呼ばれます。

一次独立な幾何ベクトルと一次従属な幾何ベクトル

いくつかの幾何ベクトルが与えられているとしましょう。 ただし、この中には零ベクトルは入っていないとします。

この内のどのベクトルも、残りのベクトルの一次結合として作ることができないとき、これらのベクトルは一次独立であるといいます。

この内のどれか一つでも、残りのベクトルの一次結合として作ることができるとき、これらのベクトルは一次従属であるといいます。

補足：一次独立、一次従属というかわりに、線型独立、線型従属という言葉が使われることもあります。

この説明ではなんだかよくわからないという人も多いかもしれませんね。そこで平面のベクトルと空間のベクトルで話を分けて、詳しく考えてみることにしましょう。

平面の幾何ベクトルの場合

1つの平面の幾何ベクトル \(\boldsymbol{a}\) があり、これは零ベクトルではないとします。ベクトルが1つしかないので、幾何ベクトル \(\boldsymbol{a}\) を残りのベクトルの一次結合で作るということは当然できません。つまり、これは一次独立です。

2つの平面の幾何ベクトル \(\boldsymbol{a}, \boldsymbol{b}\) がありどちらも零ベクトルではないとします。 実は、\(\boldsymbol{a}, \boldsymbol{b}\) が平行ならばこれらは一次従属で、平行でないならばこれらは一次独立です。
なぜなら、\(\boldsymbol{a}, \boldsymbol{b}\) が平行なら片方のベクトルを（必要なら負の数を使って）ナントカ倍すれば残りのベクトルになるわけですし、\(\boldsymbol{a}, \boldsymbol{b}\) が平行でないならどちらのベクトルを何倍しても残りのベクトルにはならないからです。

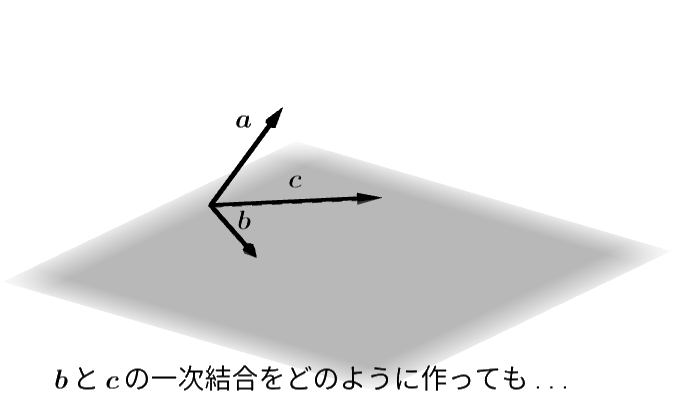
3つの平面の幾何ベクトル \(\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c}\) がありどれも零ベクトルではないとします。 実は、このとき必ずこれらのベクトルは一次従属です。 次の図を見るとわかるように、どれか一つのベクトルは必ず残りのベクトルの一次結合として作ることができるからです。

前へ 次へ

空間の幾何ベクトルの場合

空間の中の矢印を想像しながら以下を読んでください。

1つの空間の幾何ベクトル \(\boldsymbol{a}\) があり零ベクトルではないとします。平面のときと同じ理由でこれは一次独立です。

2つの空間のベクトル \(\boldsymbol{a}, \boldsymbol{b}\) がありどちらも零ベクトルではないとします。 これらが平行ならばこれらは一次従属で、平行でないならばこれらは一次独立です。 これも平面のときと全く同じ理由によります。

3つの空間のベクトル \(\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c}\) がありどれも零ベクトルではないとします。 \(\boldsymbol{a}, \boldsymbol{b},\boldsymbol{c}\) をあらわす矢印をうまく平行移動して、すべてある同じ平面の中に置くことができればこれらは一次従属で、そのようにできなければこれらは一次独立です。
なぜなら、\(\boldsymbol{a}, \boldsymbol{b},\boldsymbol{c}\) がある同じ平面の中にあれば（平面の場合で説明したように）どのベクトルも必ず残りのベクトルの一次結合として作ることができます。

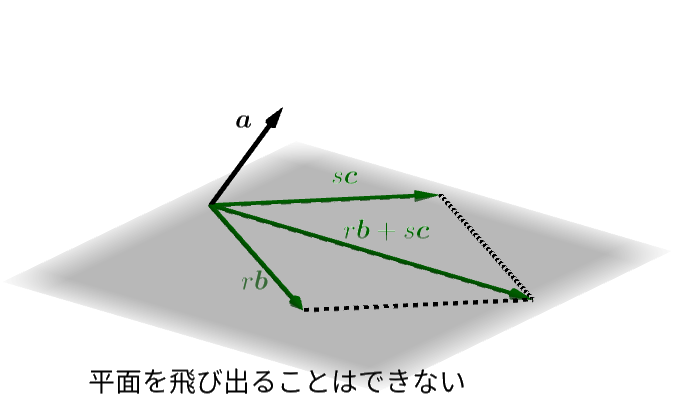
しかし、これら3つのうち、どれか1つでも同じ平面の中に置くことができなければどのベクトルも残りのベクトルの一次結合として作ることはできません。 この3つベクトルのうち同じ平面に乗せることができるのは2つですが、それら2つの一次結合をどのように作ってもその平面を飛び出す矢印はできないからです。 このことを次のスライドで確認してみましょう。

前へ 次へ

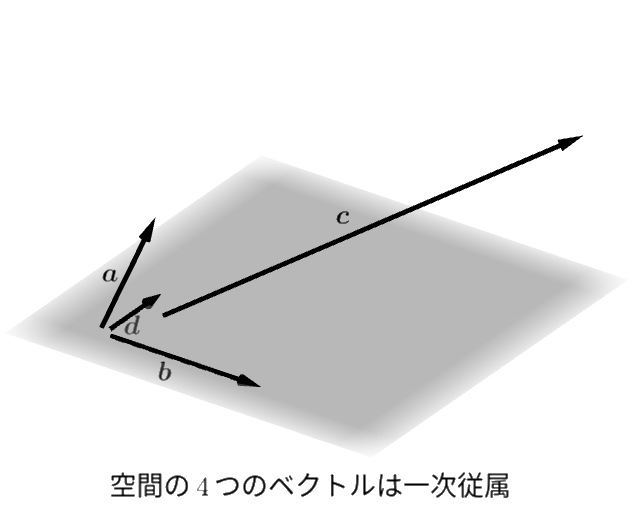
こんどは4つの平面のベクトル \(\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c}, \boldsymbol{d}\) がありどれも零ベクトルではないとします。 実は、このとき必ずこれらのベクトルは一次従属です。
次のスライドを見るとわかるように、どのベクトルも必ず残りのベクトルの一次結合として作ることができるからです。

前へ 次へ

詳しく言うと…

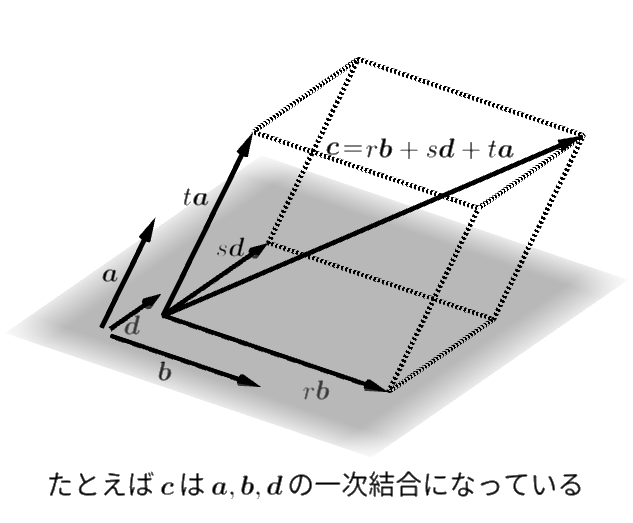
4つのベクトルの中に平行な2つのベクトルがあればもうそれだけで4つのベクトルは一次従属です。
4つのベクトルの中に1つの平面に乗せられる3つのベクトルがあればもうそれだけで4つのベクトルは一次従属です。
上の図はそれ以外の場合、つまりベクトルが3つまでなら一次独立、4つ目を仲間に入れると一次従属となる場合です。

幾何ベクトルの空間の次元と一次独立

\(V^2\) はいわゆる「2次元」の空間で \(V^3\) はいわゆる「3次元」の空間です。このような平面や空間のベクトルの空間、つまり幾何ベクトルの空間を考えているだけなら、それらの空間の次元は常識的に直感的に理解することができます。

しかしこれから扱うことになる、数学で取り扱われるもっと一般的なベクトルの空間を考える場合、ベクトルの空間の次元をもっと厳密に定義する必要がでてきます。

そこでそのような事態に備え、幾何ベクトルの空間の次元をベクトルの言葉で定義することにします。

そのときによりどころになるのは、次のような事実です。 それは、これまでの説明で想像できることですが、

• \(V^2\) では、一次独立なベクトルの最大数は \(2\)
• \(V^3\) では、一次独立なベクトルの最大数は \(3\)

となっているということです。

そこで、このことを利用して、幾何ベクトルの空間の次元を次のように定義します。

定義

\(V\) を幾何ベクトルの空間 \(V^2\) または \(V^3\) とします。 \(V\) において、一次独立なベクトルの最大数を \(V\) の次元といいます。

幾何ベクトルの空間の基底

基底とは

正確な話は後でしますが、幾何ベクトルの空間には、一次結合を作るという操作を使うことにより空間全体を支配できるいくつかのベクトルが必ずあります。そのようないくつかのベクトルを並べたものは基底と呼ばれています。

話をわかりやすくするために、ここではまず平面のベクトルの空間 \(V^2\) の場合で考えます。

\(V^2\) の次元は \(2\) で、一次独立なベクトルの最大数は \(2\) です。
そこで一次独立な2つの幾何ベクトル \(\boldsymbol{a},\boldsymbol{b}\) を用意します。（零ベクトルではなく平行ではない2つのベクトルを用意すればいいわけですね。） このとき、もう1つの平面のベクトル \(\boldsymbol{c}\) があるとしましょう。
\(V^2\) では一次独立なベクトルの最大数は \(2\) ですから、\(\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}\) は一次従属になってしまうので、ある2つの数 \(x,y\) を用いて \[ \boldsymbol{c} = x\,\boldsymbol{a}+y\,\boldsymbol{b} \]
のように、$ $ を \(\boldsymbol{a},\boldsymbol{b}\) の一次結合としてあらわすことができるはずです。

これは、\(V^2\) では、一次独立な2つのベクトル \(\boldsymbol{a},\boldsymbol{b}\) があれば、どんな \(V^2\) のベクトルも \(\boldsymbol{a},\boldsymbol{b}\) の一次結合として作ることができることを意味しています。

話を整理すると、この \(\boldsymbol{a},\boldsymbol{b}\) は次のような条件を満たしています。

• \(\boldsymbol{a},\boldsymbol{b}\) は一次独立
• どんな \(V^2\) のベクトルも \(\boldsymbol{a},\boldsymbol{b}\) の一次結合として作ることができる

そして、この2つの条件を満たしているとき、\(\boldsymbol{a},\boldsymbol{b}\) を並べたものを \(\lt\boldsymbol{a},\boldsymbol{b}\gt\) という記号であらわし、 \(V^2\) の基底といいます。

補足：とにかく、「零ベクトルではない2つのベクトルで平行ではないもの」があればそれらを並べて \(V^2\) の基底とすることができます。 つまり、\(V^2\) の基底は無数にあるわけです。
\(\lt\boldsymbol{a},\boldsymbol{b}\gt\) という記号の代わりに \(\{\boldsymbol{a},\boldsymbol{b}\}\) という記号が使われたり、場合によってはカッコが何も書かれていないこともあります。

平面に原点 \(\mathrm{O}\) と \(\mathrm{O}\) を通る直交座標系が描いてある場合は、

\[ \boldsymbol{e}_1 = \left( \begin{array}{r} 1\\ 0 \end{array} \right),\quad \boldsymbol{e}_2 = \left( \begin{array}{r} 0\\ 1 \end{array} \right) \] という2つの幾何ベクトルを並べたもの \(\lt\boldsymbol{e}_1,\boldsymbol{e}_2\gt\) を \(V\) の基底として使うと便利です。 この直交座標系の軸の名前を \(x\) 軸、\(y\) 軸と呼ぶことにすると、\(\boldsymbol{e}_1\) は \(x\) 軸のプラスの向きに \(1\) 進む矢印であらわされ、\(\boldsymbol{e}_2\) は \(y\) 軸のプラスの向きに \(1\) 進む矢印であらわされることに注意しましょう。

では、空間のベクトルの空間 \(V^3\) ではどんなものが基底になるのでしょうか。

平面の場合の説明から想像できるように、空間では、零ベクトルではない3つのベクトル \(\boldsymbol{a},\boldsymbol{b}, \boldsymbol{c}\) で、始点をそろえたときすべてがある1つの平面に乗っていないようなもの（つまり、一次独立な3つのベクトル）があれば、どんなベクトルもそれらの一次結合として作ることができます。 ですから、それらを並べたもの \(\lt\boldsymbol{a},\boldsymbol{b}, \boldsymbol{c}\gt\) が \(V^3\) の基底になります。

話を整理すると

• \(\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}\) は一次独立
• どんな \(V^3\) のベクトルも \(\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}\) の一次結合として作ることができる

という2つの条件を満たしているとき、\(\lt\boldsymbol{a},\boldsymbol{b}, \boldsymbol{c}\gt\) は \(V^3\) の基底であるということです。

空間に原点 \(\mathrm{O}\) と \(\mathrm{O}\) を通る直交座標系が描いてある場合は、平面のときと同様に、

\[ \boldsymbol{e_1} = \left( \begin{array}{r} 1\\ 0\\ 0 \end{array} \right),\quad \boldsymbol{e_2} = \left( \begin{array}{r} 0\\ 1\\ 0 \end{array} \right),\quad \boldsymbol{e_3} = \left( \begin{array}{r} 0\\ 0\\ 1 \end{array} \right) \]

という3つのベクトルを組にしたもの \(\lt\boldsymbol{e}_1,\boldsymbol{e}_2,\boldsymbol{e}_3\gt\) を \(V^3\) の基底として使うと便利です。

基底を使った幾何ベクトルと数ベクトルの対応

以前、座標系を使って 幾何ベクトルを数ベクトルに対応させることを説明しました。ここではこの考えをさらに洗練させて、（座標系の代わりに）基底を使って幾何ベクトルを数ベクトルに対応させることを考えます。

まず 平面のベクトルの空間 \(V^2\) の場合で考えてみましょう。 いま 何かしらの \(V^2\) の基底 \(\lt\boldsymbol{a},\boldsymbol{b}\gt\) があるとします。 （\(\boldsymbol{a},\boldsymbol{b}\) はどちらも零ベクトルではなく平行ではありませんね。） そうすると、\(V^2\) の どんなベクトルも \(\boldsymbol{a},\boldsymbol{b}\) の一次結合としてあらわすことができるのでしたね。つまり、\(V^2\)の どんな幾何ベクトル \(\boldsymbol{u}\) も 何かしらの 2つの数 \(x,y\) を用いて

\[\boldsymbol{u}=x\,\boldsymbol{a} + y\,\boldsymbol{b}\] とあらわされるはずです。

このとき、まず次の命題が成り立つことに注意しておきます。

命題

幾何ベクトル \(\boldsymbol{a},\boldsymbol{b}\) が一次独立のとき、零ベクトル \(\boldsymbol{0}\) を \(\boldsymbol{a},\boldsymbol{b}\) の一次結合として作る方法は \[ 0\,\boldsymbol{a} + 0\,\boldsymbol{b} \] 以外にはありません。

証明

\(\boldsymbol{a},\boldsymbol{b}\) が一次独立なので、どちらも零ベクトルではなく、この2つは平行ではありません。 ですから、これらの一次結合として零ベクトルを作りたかったら、\(0\,\boldsymbol{a} + 0\,\boldsymbol{b}\)とする以外にないことは直感的に明らかでしょう。

そしてこの命題から次の定理を導くことができます。

定理

\(V^2\) の ベクトルを基底 \(\lt\boldsymbol{a},\boldsymbol{b}\gt\) の一次結合としてあらわす仕方は一通りしかありません。

証明

\(V^2\) の ベクトル \(\boldsymbol{u}\) が

\[ \boldsymbol{u} = x_1\boldsymbol{a} + y_1\boldsymbol{b} \]

\[ \boldsymbol{u} = x_2\boldsymbol{a} + y_2\boldsymbol{b} \] のように一見二通りにあらわせたとします。 するともちろん

\[ x_1\boldsymbol{a} + y_1\boldsymbol{b} =x_2\boldsymbol{a} + y_2\boldsymbol{b} \]

であるはずなので、幾何ベクトルの演算の性質を使ってさらに式変形すると、

\[ (x_1-x_2)\boldsymbol{a} + (y_1-y_2)\boldsymbol{b}=\boldsymbol{0} \]

とできます。

\(\boldsymbol{a},\boldsymbol{b}\) は基底ですから一次独立です。 ですから前の命題より、

\[ x_1-x_2=0, \quad y_1-y_2=0 \] であることになり、 \[ x_1=x_2,\quad y_1=y_2 \] ということになります。 つまり、実は一通りにしかあらわせないことがわかります。

上の定理より \(V^2\) のどんなベクトル \(\boldsymbol{u}\) も基底 \(\lt\boldsymbol{a},\boldsymbol{b}\gt\) を使って

\[ \boldsymbol{u} = x\,\boldsymbol{a} + y\,\boldsymbol{b} \] のように一次結合としてあらわすことができ、しかも \(x,y\) の値は一通りに決まるということになります。

ですから、幾何ベクトル \(\boldsymbol{u}\) に対して1つだけ数ベクトル

\[\left( \begin{array}{r} x\\ y \end{array} \right) \] を対応させることができ、幾何ベクトルを数ベクトルとして扱うことができるようになるわけです。

空間のベクトルの空間 \(V^3\) の場合でも同様なことが言えます。

何らかの基底 \(\lt\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}\gt\) を決めておくと、\(V^3\) のベクトル \(\boldsymbol{u}\) は

\[ \boldsymbol{u} = x\,\boldsymbol{a} + y\,\boldsymbol{b}+z\boldsymbol{c} \]

のように一次結合としてあらわすことができ、しかも \(x,y,z\) の値は一通りに決まります。 ですから幾何ベクトル \(\boldsymbol{u}\) に対して1つだけ数ベクトル

\[ \left( \begin{array}{r} x\\ y\\ z \end{array} \right) \]

を対応させることができることになります。

注意：基底を別のものに取り替えると、幾何ベクトル \(\boldsymbol{u}\) に対応する数ベクトルは変ってしまいます。 そのとき数ベクトルがどのように変るのかを調べることは、線形代数学の大切なテーマの1つです。

補足：平面の場合で、右手系の直交座標系を思い浮かべてみてください。 この座標系を使って幾何ベクトルを数ベクトルに対応させたものは、実は \(V^2\) の基底として\(\lt\boldsymbol{e}_1,\boldsymbol{e}_2\gt\) を用いて幾何ベクトルを数ベクトルに対応させたものと一致します。 空間の場合でも 、右手系の直交座標系を使うと、 \(V^3\) の基底として\(\lt\boldsymbol{e}_1,\boldsymbol{e}_2,\boldsymbol{e}_3 \gt\) を使っているのと同じになります。

まとめ

いくつかの幾何ベクトル \(\boldsymbol{a},\boldsymbol{b},\ldots,\boldsymbol{c}\) に対して、いくつかの数 \(x,y,\ldots,z\) を用意し \[ x\,\boldsymbol{a}+y\,\boldsymbol{b}+\cdots+z\,\boldsymbol{c} \] というようにして作られる幾何ベクトルを \(\boldsymbol{a},\boldsymbol{b},\ldots,\boldsymbol{c}\) の一次結合といいます。

どれも \(\boldsymbol{0}\) ではないいくつかの幾何ベクトル \(\boldsymbol{a},\boldsymbol{b},\ldots,\boldsymbol{c}\) があるとします。 この内のいずれかの幾何ベクトルが残りの幾何ベクトルの一次結合としてあらわされるとき \(\boldsymbol{a},\boldsymbol{b},\ldots,\boldsymbol{c}\) は一次従属であるといい、そうではないとき一次独立であるといいます。

幾何ベクトルの空間で、一次独立なベクトルの最大数をその空間の次元といいます。 ですから \(V^2\) の次元は \(2\)、\(V^3\) の次元は \(3\) です。

幾何ベクトルの空間で、いくつかのベクトル \(\boldsymbol{a},\boldsymbol{b},\ldots,\boldsymbol{c}\) に対して、これらが一次独立でさらにどんな幾何ベクトルもこれらの一次結合としてあらわせるとき、それらを並べたもの \(\lt\boldsymbol{a},\boldsymbol{b},\ldots,\boldsymbol{c}\gt\) をその空間の基底といいます。 基底は1種類ではなく、何通りでも考えることができます。

基底を使って、幾何ベクトルに数ベクトルを対応させることができます。 基底を変えると、対応する数ベクトルは変わります。