行列とその演算(2)
2022-05-14
行列とその演算(1)では「加法」と「スカラー倍」と呼ばれる演算を定義しました。 ここではさらに、「積」と呼ばれる演算を定義します。
行列の積
普通の数の世界には「積」と呼ばれる演算があります。いわゆる「かけ算」のことです。
行列の世界でも、ある仕方で「積」と呼ばれる演算を定義することができ、行列どうしを「かけ算」できるようになります。
まず、積の特別な場合として、行ベクトルと列ベクトルの積を定義し、そのあと、行列一般に対して積を定義することにします。
行ベクトルと列ベクトルの積
ここでは、\((1,n)\) 型の行列を行ベクトル、 \((m,1)\) 型の行列を列ベクトルと呼ぶことにします。 つまり、 \[(a_1\ a_2 \ \cdots \ a_n)\] のように、1行しかない行列を行ベクトルと呼び、
\[ \left( \begin{array}{c} b_1\\ b_2\\ \vdots\\ b_m \end{array} \right) \]
のように、1列しかない行列を列ベクトルと呼ぶわけです。
このような行ベクトルと列ベクトルでは、\(m\) と \(n\) が等しい場合に限り、 \[a_1b_1+a_2b_2+\cdots a_nb_n\] という数を作ることができます。
この数を、行ベクトルと列ベクトルの積と呼ぶことにし、この積を求める計算を次のように書きあらわすことがあります。
\[ (a_1 \ a_2 \ \cdots \ a_n) \left( \begin{array}{c} b_1\\ b_2\\ \vdots\\ b_n \end{array} \right) = a_1b_1+a_2b_2+\cdots a_nb_n \]
例
\[ \begin{eqnarray} (2 \quad 8 \ -6 \ -1) \left( \begin{array}{r} 3\\ -1\\ -5\\ 0 \end{array} \right) &=& 2\times3 + 8\times (-1) +(-6)\times (-5) + (-1)\times 0\\[9pt] &=& 6-8+30+0\\[6pt] &=& 28 \end{eqnarray} \]
行列の積
2つの行列 \(A\) と \(B\) があり、\(A\) の列数と \(B\) の行数が等しくなっているとします。
つまり、ここでは、\(A\) は \((l,m)\) 型で \(B\) は \((m,n)\) 型であるとします。
このとき、以下のようにして、\(A\) と \(B\) の積と呼ばれる \((l,n)\) 型の行列を作ることができ、これを \(AB\) という記号であらわします。
行列の積のつくりかた
まず、わかりやすくするために、次のように \(A\) を行に分割し、 \(B\) を列に分割します。\[ A = \left( \begin{array}{ccccc} a_{ 11 } & a_{ 12 } & \ldots & \ldots & a_{ 1m } \\ \hline a_{ 21 } & a_{ 22 } & \ldots & \ldots & a_{ 2m } \\ \hline \vdots & \vdots & \ddots & \ddots & \vdots \\ \hline a_{ i1 } & a_{ i2 } & \ldots & \ldots & a_{ im } \\ \hline \vdots & \vdots & \ddots & \ddots & \vdots \\ \hline a_{ l1 } & a_{ l2 } & \ldots & \ldots & a_{ lm } \end{array} \right) \]
\[ B=\left( \begin{array}{c|c|c|c|c|c} b_{ 11 } & b_{ 12 } & \ldots & b_{1j} & \ldots & b_{ 1n } \\ b_{ 21 } & b_{ 22 } & \ldots & b_{2j} & \ldots& b_{ 2n } \\ \vdots & \vdots & \ddots &\vdots & \ddots& \vdots \\ \vdots & \vdots & \ddots &\vdots & \ddots& \vdots \\ b_{ m1 } & b_{ m2 } & \ldots & b_{1j} & \ldots & b_{ mn } \end{array}\right) \]
このようにすると、\(A\) は行ベクトルが縦に \(l\) 個並んでいて、 \(B\) は列ベクトルが横に \(n\) 個並んだものと思うことができます。そして、\(A\) と \(B\) の積と呼ばれ、 \(AB\) という記号であらわされることになる行列の各成分を次のような計算で作ります。
まず、\(AB\) の \((1,1)\) 成分ですが、これは、\(A\) の第 \(1\) 行ベクトルと \(B\) の第 \(1\) 列ベクトルの積を計算して作ります。 つまり、\[ \begin{eqnarray} AB\,\text{の}\,(1,1)\,\text{成分} &=&(a_{11} \ a_{12} \ \cdots \ a_{1m}) \left( \begin{array}{c} b_{11}\\ b_{21}\\ \vdots\\ b_{m1} \end{array} \right)\\[6pt] &=& a_{11}b_{11}+a_{12}b_{21}+\cdots + a_{1m}b_{m1} \end{eqnarray} \]
のように計算して作ります。
次は \(AB\) の \((1,2)\) 成分ですが、これは、\(A\) の第 \(1\) 行ベクトルと \(B\) の第 \(2\) 列ベクトルの積を計算して作ります。 つまり、\[ \begin{eqnarray} AB\,\text{の}\,(1,2)\,\text{成分} &=&(a_{11} \ a_{12} \ \cdots \ a_{1m}) \left( \begin{array}{c} b_{12}\\ b_{22}\\ \vdots\\ b_{m2} \end{array} \right) \\[6pt] &=& a_{11}b_{12}+a_{12}b_{22}+\cdots + a_{1m}b_{m2} \end{eqnarray} \]
のように計算して作ります。
さらに \(AB\) の \((1,3)\) 成分ですが、これは、\(A\) の第 \(1\) 行ベクトルと \(B\) の第 \(3\) 列ベクトルの積を計算して作ります。 つまり、\[ \begin{eqnarray} AB\,\text{の}\,(1,3)\,\text{成分} &=&(a_{11} \ a_{12} \ \cdots \ a_{1m}) \left( \begin{array}{c} b_{12}\\ b_{22}\\ \vdots\\ b_{m2} \end{array} \right) \\[6pt] &=& a_{11}b_{13}+a_{12}b_{23}+\cdots + a_{1m}b_{m3} \end{eqnarray} \]
のように計算して作ります。
この先も同様に計算を行います。
ですから、\(AB\) の \((i,j)\) 成分を作りたかったら、\(A\) の第 \(i\) 行ベクトルと \(B\) の第 \(j\) 列ベクトルの積を計算して作るわけです。つまり、 \(i=1,2,\ldots,l,\:j=1,2,\ldots,n\) に対して、
\[ \begin{eqnarray} AB\,\text{の}\,(i,j)\,\text{成分} &=& A\,\text{の第}\,i\,\text{行ベクトルと}\,B\,\text{の第}\,j\,\text{列ベクトルの積}\\[6pt] &=&(a_{i1} \ a_{i2} \ \cdots \ a_{im}) \left( \begin{array}{c} b_{1j}\\ b_{2j}\\ \vdots\\ b_{mj} \end{array} \right) \\[6pt] &=& a_{i1}b_{1j}+a_{i2}b_{2j}+\cdots a_{im}b_{mj} \end{eqnarray} \]
\[ \left( \begin{array} {cccc} (1,1) \text{成分} &(1,2) \text{成分}&…&(1,n)\text{成分}\,\\ (2,1) \text{成分} &(2,2) \text{成分} &…&(2,n)\text{成分}\,\\ \vdots & \vdots & \ddots & \vdots \\ (l,1) \text{成分} &(l,2) \text{成分}&…&(l,n)\text{成分}\, \end{array} \right) \]
を作るわけです。このようにして、\((l,m)\) 型行列 \(A\) と \((m,n)\) 型行列 \(B\) から \((l,n)\) 型行列 \(AB\) を作ることができるわけです。
以上の計算を模式的に書くと次のようになります。
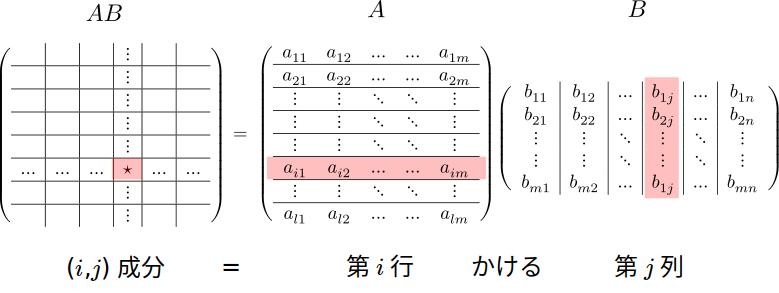
\[A = \left( \begin{array}{rrr} -2 & 3 & 0\\ \hline 2 & 1 & 2 \end{array} \right),\: B= \left( \begin{array}{r|r|r} 2 & 3 & 1\\ 0 & 2 & 1\\ -1 & -3 & 3 \end{array} \right) \]
のとき、行列 \(A\) 行列 \(B\) の積 \(AB\) を作ってみることにします。
\(A\) は \((2,3)\) 型の行列で \(B\) は \((3,3)\) 型の行列ですから、\(A\) の列数と \(B\) の行数はどちらも \(3\) で等しくなっています。ですから積 \(AB\) をつくることができ、それは \((2,3)\) 型の行列になるはずです。そして、積 \(AB\) の \((i,j)\) 成分をつくるには \(A\) の第 \(i\) 行と \(B\) の第 \(j\) 列の積を計算すればよいのでした。
このことを頭に入れておいた上で、 \(AB\) の各成分を計算することにしましょう。すると以下のようになります。\[ \begin{eqnarray} AB\,\text{の}(1,1)\text{成分} &=& -2\times2+3\times0+0\times (-1) =-4+0+0=-4\\[6pt] AB\,\text{の}(1,2)\text{成分} &=& -2\times3+3\times2+0\times (-3) =-6+6+0=0\\[6pt] AB\,\text{の}(1,3)\text{成分} &=& -2\times1+3\times1+0\times 3 =-2+3+0=1\\[6pt] AB\,\text{の}(2,1)\text{成分} &=& 2\times2+1\times0+2\times (-1) =4+0-2=2\\[6pt] AB\,\text{の}(2,2)\text{成分} &=& 2\times3+1\times2+2\times (-3) =6+2-6=2\\[6pt] AB\,\text{の}(2,3)\text{成分} &=& 2\times1+1\times1+2\times 3 =2+1+6=9 \end{eqnarray} \]
となるので、 \[ AB = \left( \begin{array}{rrr} -4 & 0 & 1\\ 2 & 2 & 9 \end{array} \right) \] となるわけです。
まとめ
行ベクトルと列ベクトルがあるとします。行ベクトルの成分の数と列ベクトルの成分の数が等しいときに限ってその行ベクトルと列ベクトルの積を定義することができます。
2つの行列 \(A\) と \(B\) があるとします。\(A\) の列数と \(B\) の行数が等しいときに限って \(A\) と \(B\) の積 \(AB\) を定義することができます。\(AB\) の \((i,j)\) 成分は \(A\) の第 \(i\) 行ベクトルと \(B\) の第 \(j\) 列ベクトルの積として定義します。